# This should install any required dependencies assuming JAX has already been installed
try:
    import luas
except ImportError:
    !git clone https://github.com/markfortune/luas.git
    %cd luas
    %pip install .
    %cd ..

try:
    import jaxoplanet
except ImportError:
    %pip install -q jaxoplanet==0.0.1

try:
    import pymc
except ImportError:
    %pip install -q pymc
    
try:
    import corner
except ImportError:
    %pip install -q corner
    
try:
    import arviz as az
except ImportError:
    %pip install -q arviz

PyMC Example: Transmission Spectroscopy

NOTE: This tutorial notebook is currently in development. Expect significant changes in the future

This notebook provides to tutorial on how to use PyMC to perform spectroscopic transit light curve fitting. We will first go through how to generate transit light curves in jax, then we will create synthetic noise which will be correlated in both wavelength and time. Finally we will use PyMC to fit the noise contaminated light curves and recover the input transmission spectrum. You can run this notebook yourself on Google Colab by clicking the rocket icon in the top right corner.

If you have a GPU available (including a GPU on Google Colab) then jax should detect this and run on it automatically. Running jax.devices() tells us what jax has found to run on. If there is a GPU available but it is not detected this could indicate jax has not been correctly installed for GPU. Also note if running on Google Colab that the T4 GPUs have poor performance at double precision floating point and may not show significant speed-ups, while more modern hardware such as NVIDIA Tesla V100s or better tend to show significant performance improvements

import numpy as np
import jax
import jax.numpy as jnp
import matplotlib.pyplot as plt
import os.path
import logging
from jaxoplanet.orbits import KeplerianOrbit
from jaxoplanet.light_curves import QuadLightCurve
import arviz as az
import pandas as pd

# Useful to set when looking at retrieved values for many parameters
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)

# This helps give more information on what PyMC is doing during inference
logging.getLogger().setLevel(logging.INFO)

# Running this at the start of the runtime ensures jax uses 64-bit floating point numbers
# as jax uses 32-bit by default
jax.config.update("jax_enable_x64", True)

# This will list available CPUs/GPUs JAX is picking up
print("Available devices:", jax.devices())

Available devices: [CpuDevice(id=0)]

INFO:absl:Remote TPU is not linked into jax; skipping remote TPU.
INFO:absl:Unable to initialize backend 'tpu_driver': Could not initialize backend 'tpu_driver'
INFO:absl:Unable to initialize backend 'cuda': module 'jaxlib.xla_extension' has no attribute 'GpuAllocatorConfig'
INFO:absl:Unable to initialize backend 'rocm': module 'jaxlib.xla_extension' has no attribute 'GpuAllocatorConfig'
INFO:absl:Unable to initialize backend 'tpu': module 'jaxlib.xla_extension' has no attribute 'get_tpu_client'

First we will use jaxoplanet which has its own documentation and tutorials here. Let’s create a single light curve with quadratic limb darkening. We will use the transit_light_curve function from luas.exoplanet which we have included below to show what it does.

def transit_light_curve(par, t):
    """Uses the package `jaxoplanet <https://github.com/exoplanet-dev/jaxoplanet>`_ to calculate
    transit light curves using JAX assuming quadratic limb darkening and a simple circular orbit.
    
    This particular function will only compute a single transit light curve but JAX's vmap function
    can be used to calculate the transit light curve of multiple wavelength bands at once.
    
    Args:
        par (PyTree): The transit parameters stored in a PyTree/dictionary (see example above).
        t (JAXArray): Array of times to calculate the light curve at.
            
    Returns:
        JAXArray: Array of flux values for each time input.
        
    """
    
    light_curve = QuadLightCurve.init(u1=par["u1"], u2=par["u2"])
    orbit = KeplerianOrbit.init(
        time_transit=par["T0"],
        period=par["P"],
        semimajor=par["a"],
        impact_param=par["b"],
        radius=par["rho"],
    )
    
    flux = (par["Foot"] + 24*par["Tgrad"]*(t-par["T0"]))*(1+light_curve.light_curve(orbit, t)[0])
    
    return flux

from luas.exoplanet import transit_light_curve

# Let's use the literature values used in Gibson et al. (2017) to start us off
mfp = {
    "T0":0.,     # Central transit time
    "P":3.4,     # Period (days)
    "a":8.,      # Semi-major axis to stellar ratio aka a/R*
    "rho":0.1,   # Radius ratio rho aka Rp/R*
    "b":0.5,     # Impact parameter
    "u1":0.5,    # First quadratic limb darkening coefficient
    "u2":0.1,    # Second quadratic limb darkening coefficient
    "Foot":1.,   # Baseline flux out of transit
    "Tgrad":0.   # Gradient in baseline flux (hrs^-1)
}

# Generate 100 evenly spaced time points (in units of days)
N_t = 100
x_t = jnp.linspace(-0.15, 0.15, N_t)

plt.plot(x_t, transit_light_curve(mfp, x_t), "k.")
plt.xlabel("Time (days)")
plt.ylabel("Normalised Flux")
plt.show()

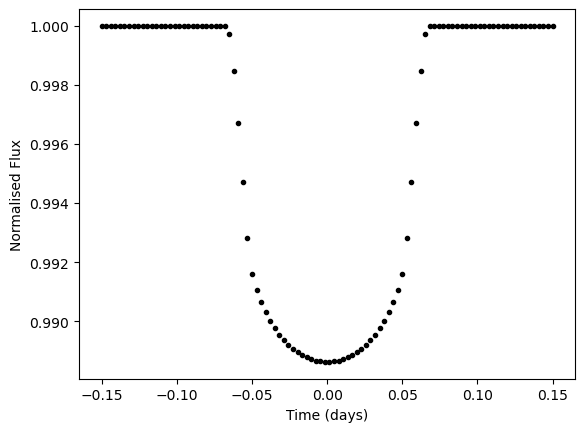
Now we want to take our jax function which has been written to generate a 1D light curve in time and instead create separate light curves in each wavelength. We also will want to share some parameters between light curves (e.g. impact parameter b, system scale a/Rs) while varying other parameters for each wavelength (e.g. radius ratio Rp/Rs).

We could of course write a for loop but for loops can be slow to compile with jax. A more efficient option is to make use of the jax.vmap function which allows us to “vectorise” our function from 1D to 2D:

# First we must tell JAX which parameters of the function we want to vary for each light curve
# and which we want to be shared between light curves
transit_light_curve_vmap = jax.vmap(
    # First argument is the function to vectorise
    transit_light_curve, 
    
    # Specify which parameters to share and which to vary for each light curve
    in_axes=(
        {
        # If a parameter is to be shared across each light curve then it should be set to None
        "T0":None, "P":None, "a":None, "b":None,

        # Parameters which vary in wavelength are given the dimension of the array to expand along
        # In this case we are expanding from 0D arrays to 1D arrays so this must be 0
        "rho":0, "u1":0, "u2":0, "Foot":0, "Tgrad":0
        },
        # Also must specify that we will share the time array (the second function parameter)
        # between light curves
         None,  
    ),
    
    # Specify the output dimension to expand along, this will default to 0 anyway
    # Will output extra flux values for each light curve as additional rows
    out_axes = 0,
)

# Let's define a wavelength range of our data, this isn't actually used by our mean function
# but we will use it for defining correlation in wavelength later
N_l = 16 # Feel free to vary the number of light curves, even >100 light curves may perform quite efficiently
x_l = np.linspace(4000, 7000, N_l)

# Now we define our 2D transit parameters, let's just assume everything is constant in wavelength
mfp_2D = {
    "T0":0.,                         # Central transit time
    "P":3.4,                         # Period (days)
    "a":8.,                          # Semi-major axis to stellar ratio aka a/R*
    "rho":0.1*np.ones(N_l),          # Radius ratio rho aka Rp/R*
    "b":0.5,                         # Impact parameter
    "u1":np.linspace(0.7, 0.4, N_l), # First quadratic limb darkening coefficient
    "u2":np.linspace(0.1, 0.2, N_l), # Second quadratic limb darkening coefficient
    "Foot":1.*np.ones(N_l),          # Baseline flux out of transit
    "Tgrad":0.*np.ones(N_l)          # Gradient in baseline flux (days^-1)
}

# Call our new vmap of transit_light_curve to simultaneously compute light curves for all wavelengths
transit_model_2D = transit_light_curve_vmap(mfp_2D, x_t)

# Visualise the transit light curves
plt.imshow(transit_model_2D, aspect = 'auto', extent = [x_t[0], x_t[-1], x_l[-1], x_l[0]])
plt.xlabel("Time (days)")
plt.ylabel("Wavelength ($\AA$)")
plt.show()

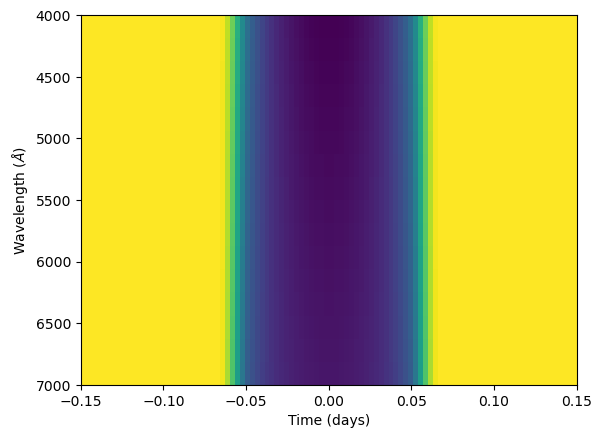
The form of a mean function with luas.GP is f(par, x_l, x_t) where par is a PyTree, x_l is a JAXArray of inputs that lie along the wavelength/vertical dimension of the data (e.g. an array of wavelength values) and x_t is a JAXArray of inputs that lie along the time/horizontal dimension (e.g. an array of timestamps). Our transit model does not require wavelength values to be computed but we still write our wrapper function to be of this form.

We will also switch to the Kipping (2013) limb darkening parameterisation as it makes it easier to place simple bounds on these parameters and has the benefit of placing a uniform prior on the physically allowed space of limb darkening parameters.

Also feel free to use the luas.exoplanet.transit_2D function instead which is similar to the below function with the exception that it fits for transit depth \(d = \rho^2\) instead of radius ratio \(\rho\)

from luas.exoplanet import ld_to_kipping, ld_from_kipping

def transit_light_curve_2D(p, x_l, x_t):
    
    # vmap requires that we only input the parameters which have been explicitly defined how they vectorise
    transit_params = ["T0", "P", "a", "rho", "b", "Foot", "Tgrad"]
    mfp = {k:p[k] for k in transit_params}
    
    # Calculate limb darkening coefficients from the Kipping (2013) parameterisation.
    mfp["u1"], mfp["u2"] = ld_from_kipping(p["q1"], p["q2"])
    
    # Use the vmap of transit_light_curve to calculate a 2D array of shape (M, N) of flux values
    # For M wavelengths and N time points.
    return transit_light_curve_vmap(mfp, x_t)


# Switch to Kipping parameterisation
if "u1" in mfp_2D:
    mfp_2D["q1"], mfp_2D["q2"] = ld_to_kipping(mfp_2D["u1"], mfp_2D["u2"])
    del mfp_2D["u1"]
    del mfp_2D["u2"]

# This should produce the same result as transit_light_curve_vmap as we have only changed the limb darkening parameterisation
M = transit_light_curve_2D(mfp_2D, x_l, x_t)

Now that we have our mean function created, it’s time to start building a kernel function. We will try keep things simple and use a squared exponential kernel for correlation in both time and wavelength, and white noise which varies in amplitude between different light curves.

\[ \begin{equation} \mathbf{K}_{ij} = h^2 \exp\left(-\frac{|\lambda_i - \lambda_j|^2}{2 l_\mathrm{\lambda}^2}\right) \exp\left(-\frac{|t_i - t_j|^2}{2 l_{t}^2}\right) + \sigma_{\lambda_i}^2\delta_{\lambda_i \lambda_j} \delta_{t_i t_j} \end{equation} \]

This kernel contains a correlated noise component with height scale \(h\), length scale in wavelength \(l_\mathrm{\lambda}\) and length scale in time \(l_t\). There is also a white noise term which can have different white noise amplitudes at different wavelengths.

We will need to write this kernel as separate wavelength and time kernel functions multiplied together satisfying:

\[ \begin{equation} \text{K}(\Delta \lambda, \Delta t) = \text{K}_{l}(\Delta \lambda) \otimes \text{K}_{t}(\Delta t) + \text{S}_{l}(\Delta \lambda) \otimes \text{S}_{t}(\Delta t) \end{equation} \]

We can do this by choosing the equations below for our kernel functions which generate each component matrix.

\[ \begin{equation} \text{K}_l(\lambda_i, \lambda_j) = h^2 \exp\left(-\frac{|\lambda_i - \lambda_j|^2}{2 l_\mathrm{\lambda}^2}\right) \end{equation} \]

\[ \begin{equation} \text{K}_t(t_i, t_j) = \exp\left(-\frac{|t_i - t_j|^2}{2 l_{t}^2}\right) \end{equation} \]

\[ \begin{equation} \text{S}_l(\lambda_i, \lambda_j) = \sigma_{\lambda_i}^2\delta_{\lambda_i \lambda_j} \end{equation} \]

\[ \begin{equation} \text{S}_t(t_i, t_j) = \delta_{t_i t_j} \end{equation} \]

Note that for numerical stability reasons it’s important that the \(S_l\) and \(S_t\) matrices are well-conditioned (i.e. can be stably inverted) while \(K_l\) and \(K_t\) do not need to be well-conditioned (or even invertible). The matrices which contain values added along the diagonal should be well-conditioned as this “regularises” the matrices, while a squared exponential kernel with nothing added along the diagonal is unlikely to be well-conditioned.

from luas import kernels
from luas import LuasKernel, GeneralKernel

# We implement each of these kernel functions below using the luas.kernels module
# for an implementation of the squared exponential kernel

# The wavelength kernel functions take the wavelength regression variable(s) x_l as input (of shape (N_l) or (d_l, N_l))
def Kl_fn(hp, x_l1, x_l2, wn = True):
    Kl = jnp.exp(2*hp["log_h"])*kernels.squared_exp(x_l1, x_l2, jnp.exp(hp["log_l_l"]))
    return Kl

# The time kernel functions take the time regression variable(s) x_t as input (of shape (N_t) or (d_t, N_t))
def Kt_fn(hp, x_t1, x_t2, wn = True):
    return kernels.squared_exp(x_t1, x_t2, jnp.exp(hp["log_l_t"]))

# For both the Sl and St functions we set a decomp attribute to "diag" because they produce diagonal matrices
# This speeds up the log likelihood calculations as it tells luas these matrices are easy to eigendecompose
# But don't do this for the Kl and Kt functions even if they produce diagonal matrices unless you know what you are doing
# This is because you are telling luas that the transformations of Kl and Kt are diagonal, not Kl and Kt themselves

# If the wn keyword argument is True then white noise should be included (doesn't affect most matrices)
# This is used by gp.predict when performing Gaussian process prediction
# Note it does not matter that Sl is not invertible without white noise
def Sl_fn(hp, x_l1, x_l2, wn = True):
    Sl = jnp.zeros((x_l1.shape[-1], x_l2.shape[-1]))
    
    if wn:
        # If we are including white noise then safe to assume Sl is a square matrix for any calculations in luas.GP
        Sl += jnp.diag(jnp.exp(2*hp["log_sigma"])) # Assumes hp["log_sigma"] is an array of size N_l

    return Sl
Sl_fn.decomp = "diag" # Sl is a diagonal matrix

def St_fn(p, x_t1, x_t2, wn = True):
    return jnp.eye(x_t1.shape[-1])
St_fn.decomp = "diag" # St is a diagonal matrix

# Build a LuasKernel object using these component kernel functions
# The full covariance matrix applied to the data will be K = Kl KRON Kt + Sl KRON St
kernel = LuasKernel(Kl = Kl_fn, Kt = Kt_fn, Sl = Sl_fn, St = St_fn,
                    
                    # Can select whether to use previously calculated eigendecompositions when running MCMC
                    # Performs an additional check in each step to see if each component covariance matrix has changed since last step
                    # Useful when doing blocked Gibbs or if fixing some hyperparameters
                    use_stored_values = True, 
                   )

# We can also add a general kernel using the same kernel function as the LuasKernel but without the kronecker product optimisations
# We will use this to show they produce the same answers and to compare runtimes
# While it takes the LuasKernel.K function, this simply takes Kl_fn, Kt_fn, Sl_fn and St_fn and kronecker products the results together
# So it builds the same covariance matrix but the log likelihood calculations are completely different
general_kernel = GeneralKernel(K = kernel.K)

The LuasKernel.visualise_covariance_matrix method should be a useful way of visualising each of the four component matrices and ensure everything you have written looks right

hp = {
    "log_h":np.log(2e-3),
    "log_l_l":np.log(1000.),
    "log_l_t":np.log(0.011),
    "log_sigma":np.log(5e-4)*np.ones(N_l),
}

kernel.visualise_covariance_matrix(hp, x_l, x_t);

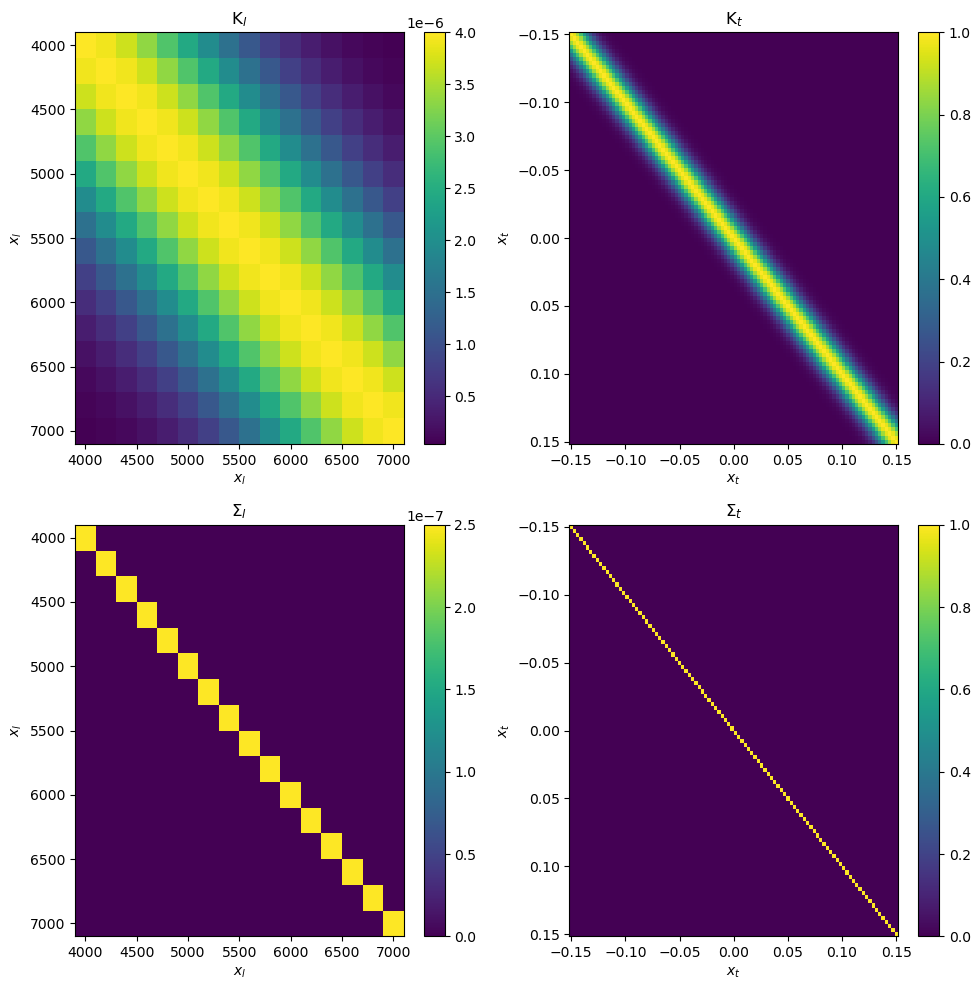
We can test the numerical stability of both the LuasKernel and GeneralKernel with a simple test where we multiply a random normal vector by the inverse of the covariance matrix followed by multiplying by the covariance matrix. This should result in the original random normal vector we started with. We should expect some level of floating point errors but they are likely to be negligible relative to the noise level in a dataset. So far I have yet to see the LuasKernel perform poorly for any valid covariance matrix. If having issues here it is worth making sure that each covariance matrix generates a symmetric covariance matrix and that \(S_l\) and \(S_t\) are invertible.

# Generate a random normal vector
random_vec = np.random.normal(size = (N_l, N_t))

# Calculate alpha = K_inv @ random_vec
alpha = kernel.K_inv_by_vec(hp, x_l, x_t, random_vec)

# Calculate K @ alpha which should equal random_vec
K_K_inv_random_vec = kernel.K_by_vec(hp, x_l, x_t, alpha)

# Calculate the numerical errors from the original vector
calc_err = random_vec - K_K_inv_random_vec
print(f"Largest deviations (LuasKernel): {calc_err.min()}, {calc_err.max()}")

# Perform the same calculation with the general_kernel which builds the full covariance matrix
# and uses Cholesky decomposition for inverting the covariance matrix
K_inv_random_vec = general_kernel.K_inv_by_vec(hp, x_l, x_t, random_vec)
K_K_inv_random_vec = general_kernel.K_by_vec(hp, x_l, x_t, K_inv_random_vec)

calc_err = random_vec - K_K_inv_random_vec
print(f"Largest deviations (GeneralKernel): {calc_err.min()}, {calc_err.max()}")

Largest deviations (LuasKernel): -2.773337115513641e-13, 1.886407696716219e-13
Largest deviations (GeneralKernel): -2.701172618913006e-13, 3.1530333899354446e-13

Take a random noise draw from this covariance matrix. Try playing around with these values to see the effect varying each parameter has on the noise generated.

hp = {"log_h":jnp.log(2e-3),
      "log_l_l":jnp.log(1000.), 
      "log_l_t":jnp.log(0.011),
      "log_sigma":jnp.log(5e-4)*jnp.ones(N_l),}

sim_noise = kernel.generate_noise(hp, x_l, x_t)

plt.imshow(sim_noise, aspect = 'auto', extent = [x_t[0], x_t[-1], x_l[-1], x_l[0]])
plt.xlabel("Time (days)")
plt.ylabel("Wavelength ($\AA$)")
plt.show()

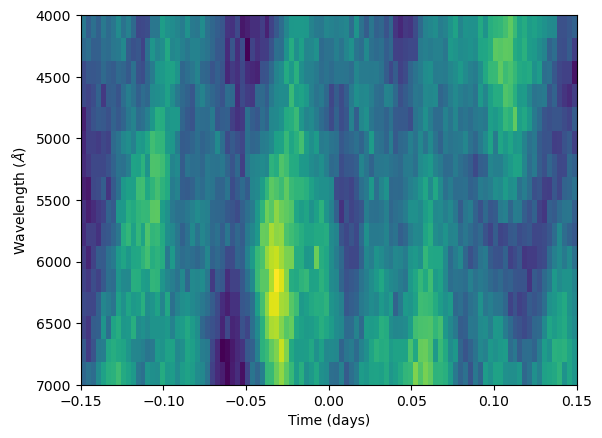
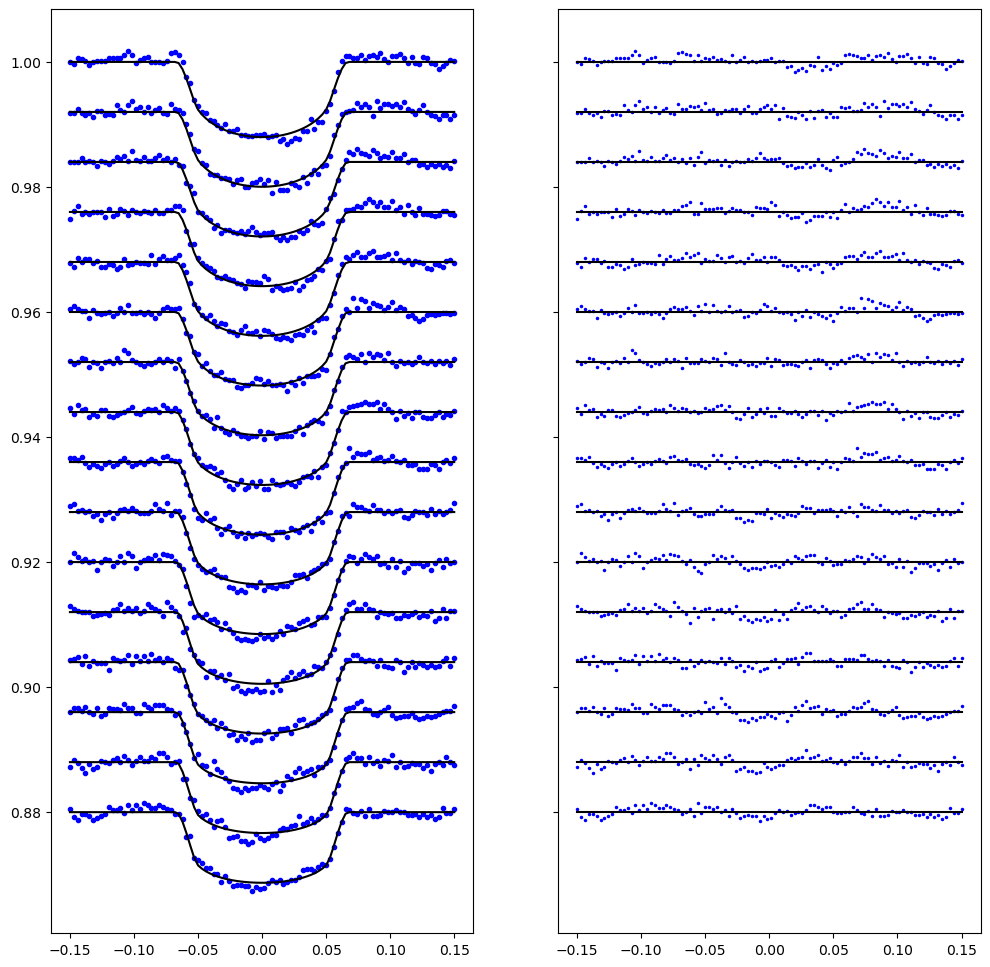
Combining our light curves and noise model we can generate synthetic light curves contaminated by systematics correlated in time and wavelength

def plot_lightcurves(x_t, M, Y, sep = 0.008):
    """Quick function to visualise light curves and the residuals after subtraction of transit model
    
    """
    N_l = x_l.shape[-1]
    
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 12), sharey = True)
    for i in range(N_l):
        ax1.plot(x_t, Y[i, :] + np.arange(0, -sep*N_l, -sep)[i], 'bo', ms = 3)
        
        ax1.plot(x_t, M[i, :] + np.arange(0, -sep*N_l, -sep)[i], 'k-', ms = 3)
        ax2.plot(x_t, Y[i, :] - M[i, :] + np.arange(1, 1-sep*N_l, -sep)[i], 'b.', ms = 3)
        ax2.plot(x_t, np.arange(1, 1-sep*N_l, -sep)[i]*np.ones_like(x_t), 'k-', ms = 3)

u1_sim, u2_sim = np.linspace(0.7, 0.4, N_l), np.linspace(0.1, 0.2, N_l)
q1_sim, q2_sim = ld_to_kipping(u1_sim, u2_sim)

# All parameters used to generate the synthetic data set with noise
# PyMC will not work with jax arrays as inputs so we are using NumPy arrays
# Our PyMC wrapper also assumes that each input is an array so convert floats to size 1 NumPy arrays
p_sim = {
    # Mean function parameters
    "T0":0.*np.ones(1),                      # Central transit time
    "P":3.4*np.ones(1),                      # Period (days)
    "a":8.*np.ones(1),                       # Semi-major axis to stellar ratio aka a/R*
    "rho":0.1*np.ones(N_l),                  # Radius ratio rho aka Rp/R* for each wavelength
    "b":0.5*np.ones(1),                      # Impact parameter
    "q1":q1_sim,                              # First quadratic limb darkening coefficient for each wavelength
    "q2":q2_sim,                              # Second quadratic limb darkening coefficient for each wavelength
    "Foot":1.*np.ones(N_l),                  # Baseline flux out of transit for each wavelength
    "Tgrad":0.*np.ones(N_l),                 # Gradient in baseline flux for each wavelength (days^-1)
    
    # Hyperparameters
    "log_h":np.log(5e-4)*np.ones(1),        # log height scale
    "log_l_l":np.log(1000.)*np.ones(1),     # log length scale in wavelength
    "log_l_t":np.log(0.011)*np.ones(1),     # log length scale in time
    "log_sigma":np.log(5e-4)*np.ones(N_l),  # log white noise amplitude for each wavelength
}

transit_signal = transit_light_curve_2D(p_sim, x_l, x_t)
sim_noise = kernel.generate_noise(p_sim, x_l, x_t)
Y = transit_signal*(1 + sim_noise)

plot_lightcurves(x_t, transit_signal, Y)

We may also want to define a logPrior function. While PyMC can also be used to define priors on parameters, it can be useful to let luas.GP handle non-uniform priors when it comes to MCMC tuning (as will be shown later).

The logPrior function input to luas.GP should be written in JAX and must be of the form logPrior(params) i.e. it may only take the PyTree of mean function parameters and hyperparameters as input.

a_mean = p_sim["a"]
a_std = 0.1
b_mean = p_sim["b"]
b_std = 0.01

# Set some limb darkening priors, normally these might be generated from a package like LDTk
u1_mean = u1_sim
u1_std = 0.01
u2_mean = u2_sim
u2_std = 0.01

def logPrior(p):
    logPrior = -0.5*((p["a"] - a_mean)/a_std)**2
    logPrior += -0.5*((p["b"] - b_mean)/b_std)**2
    
    u1, u2 = ld_from_kipping(p["q1"], p["q2"])
    u1_priors = -0.5*((u1 - u1_mean)/u1_std)**2
    u2_priors = -0.5*((u2 - u2_mean)/u2_std)**2
    
    logPrior += u1_priors.sum() + u2_priors.sum()

    return logPrior.sum()

print("Log prior at simulated values:", logPrior(p_sim))

Log prior at simulated values: -1.6370404527291505e-28

We now have enough to define our luas.GP object and use it to try recover the original transmission signal injected into the correlated noise.

from luas import GP
from copy import deepcopy

# Initialise our GP object
# Make sure to include the mean function and log prior function if you're using them
gp = GP(kernel,  # Kernel object to use
        x_l,     # Regression variable(s) along wavelength/vertical dimension
        x_t,     # Regression variable(s) along time/horizontal dimension
        mf = transit_light_curve_2D,  # (optional) mean function to use, defaults to zeros
        logPrior = logPrior           # (optional) log prior function, defaults to zero
       )

# Initialise our starting values as the true simulated values
p_initial = deepcopy(p_sim)

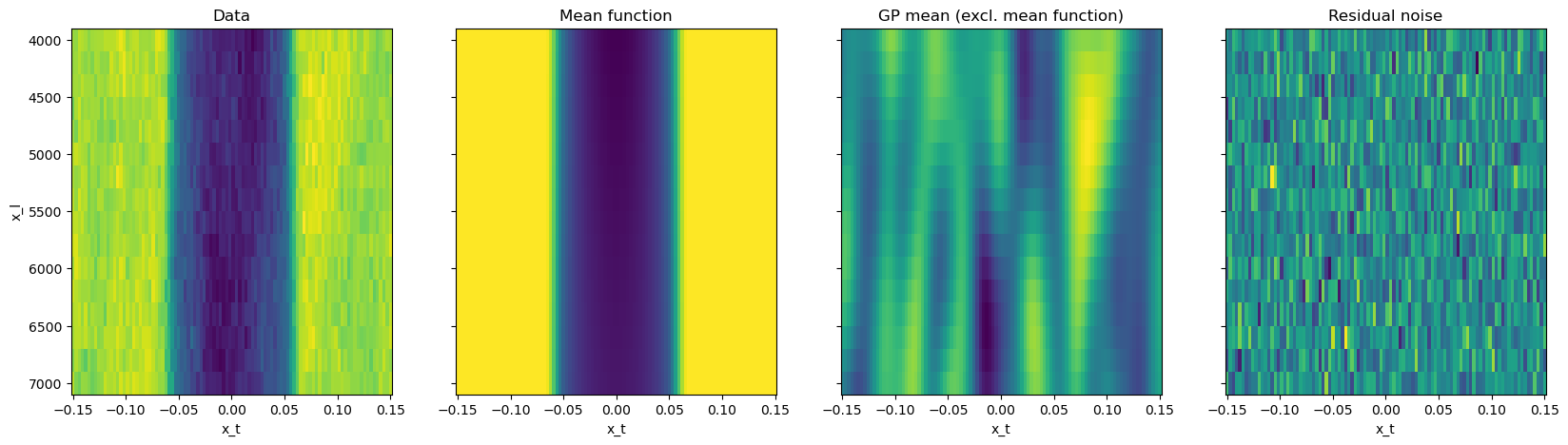
# Convenient function for plotting the data and the GP fit to the data
gp.plot(p_initial, Y)
print("Starting log posterior value:", gp.logP(p_initial, Y))

Starting log posterior value: 9804.566510790806

Let’s compare the runtime speed-up of using the optimisations in the LuasKernel. Comparing runtimes with JAX is a little bit more involved than normal. First we want to pre-compile the functions using jax.jit so that we aren’t timing how long each function takes to compile. We then must make sure we run the JIT-compiled functions once before benchmarking as the compilation step will be done based on the array sizes given in that first run. We then can time the JIT-compiled functions but make sure to include block_until_ready due to jax using asynchronous dispatch (i.e. it waits until the calculation has actually finished).

Note that while the runtime improvement for this small data set may not be substantial, the methods have very different scaling with GeneralKernel.logP scaling as \(\mathcal{O}(N_l^3 N_t^3)\) and LuasKernel.logP scaling as \(\mathcal{O}(N_l^3 + N_t^3 + N_l N_t (N_l + N_t))\), so for larger data sets the difference may be much larger. GeneralKernel.logP may also crash for larger data sets due to its higher memory requirements.

# Create a similar GP object but using general Cholesky calculations in GeneralKernel instead of using LuasKernel
gp_general = GP(general_kernel,  # Kernel object to use
        x_l,     # Regression variable(s) along wavelength/vertical dimension
        x_t,     # Regression variable(s) along time/horizontal dimension
        mf = transit_light_curve_2D,  # (optional) mean function to use, defaults to zeros
        logPrior = logPrior           # (optional) log prior function, defaults to zero
       )

# Let's JIT compile each function before running (this should already be done in GP.py but is good practice anyway)
general_jit = jax.jit(gp_general.logP)
luas_jit = jax.jit(gp.logP)

# Run each calculation before benchmarking, note they should give the same answer up to floating point errors
print("GeneralKernel Calculation:", general_jit(p_initial, Y))
print("LuasKernel Calculation:", luas_jit(p_initial, Y))

# Benchmark each method
print("\nRuntime for GeneralKernel: ")
%timeit general_jit(p_initial, Y).block_until_ready()

print("Runtime for LuasKernel: ")
%timeit luas_jit(p_initial, Y).block_until_ready()

GeneralKernel Calculation: 9804.566510790808
LuasKernel Calculation: 9804.566510790806

Runtime for GeneralKernel: 
34.1 ms ± 6.61 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Runtime for LuasKernel: 
7.43 ms ± 712 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Now let’s begin using PyMC to perform a best-fit. We’ve set the true simulated values as our initial values so we should already be close to the optimal log posterior value but for real data this won’t always be the case. Similar to the approach in Fortune et al. (2024) we will not be performing any white light curve analysis but instead will be joint-fitting all spectroscopic light curves simultaneously.

import pymc as pm
from luas.pymc_ext import LuasPyMC

# Let's define some bounds
min_log_l_l = np.log(np.diff(x_l).min())
max_log_l_l = np.log(50*(x_l[-1] - x_l[0]))
min_log_l_t = np.log(np.diff(x_t).min())
max_log_l_t = np.log(3*(x_t[-1] - x_t[0]))

# Note with PyMC that the parameter bounds must also be NumPy arrays
param_bounds = {
                # Bounds from Kipping (2013) at just between 0 and 1
                "q1":[np.array([0.]*N_l), np.array([1.]*N_l)],
                "q2":[np.array([0.]*N_l), np.array([1.]*N_l)],
    
                # Can optionally include bounds on other mean function parameters
                # but often they will be well constrained by the data
                "rho":[np.array([0.]), np.array([1.]*N_l)],
    
                # Sometimes prior bounds on hyperparameters are important for sampling
                # However their choice can sometimes affect the results so use with caution
                "log_h":   [np.log(1e-6)*np.ones(1), np.log(1)*np.ones(1)],
                "log_l_l": [min_log_l_l*np.ones(1), max_log_l_l*np.ones(1)],
                "log_l_t": [min_log_l_t*np.ones(1), max_log_l_t*np.ones(1)],
                "log_sigma":[np.log(1e-6)*np.ones(N_l), np.log(1e-2)*np.ones(N_l)],
}

# Make a wrapper function which returns a PyMC model with a given set of fixed parameters and observations Y
def transit_model(p_fixed, Y):
    
    with pm.Model() as model:

        # Makes of copy of any parameters to be kept fixed during sampling
        var_dict = deepcopy(p_fixed)
        
        # Specify the parameters we've given bounds for
        var_dict["rho"] = pm.Uniform('rho', lower=param_bounds["rho"][0],
                                     upper=param_bounds["rho"][1], shape=N_l)
        var_dict["q1"] = pm.Uniform('q1', lower=param_bounds["q1"][0],
                                    upper=param_bounds["q1"][1], shape=N_l)
        var_dict["q2"] = pm.Uniform('q2', lower=param_bounds["q2"][0],
                                    upper=param_bounds["q2"][1], shape=N_l)
        var_dict["log_h"] =   pm.Uniform("log_h", lower=param_bounds["log_h"][0],
                                         upper=param_bounds["log_h"][1], shape=1)
        var_dict["log_l_l"] = pm.Uniform("log_l_l", lower = param_bounds["log_l_l"][0],
                                         upper = param_bounds["log_l_l"][1], shape=1)
        var_dict["log_l_t"] = pm.Uniform("log_l_t", lower = param_bounds["log_l_t"][0],
                                         upper = param_bounds["log_l_t"][1], shape=1)
        var_dict["log_sigma"] = pm.Uniform('log_sigma', lower=param_bounds["log_sigma"][0],
                                           upper=param_bounds["log_sigma"][1], shape=N_l)
        
        # Specify the unbounded parameters
        var_dict["T0"] = pm.Flat('T0', shape=1)
        var_dict["a"] = pm.Flat('a', shape=1)
        var_dict["b"] = pm.Flat('b', shape=1)
        var_dict["Foot"] = pm.Flat('Foot', shape=N_l)
        var_dict["Tgrad"] = pm.Flat('Tgrad', shape=N_l)

        # PyMC wrapper for luas log posterior calculations
        # Requires the gp object, a dictionary of each model parameter and the observations Y
        LuasPyMC("log_like", gp = gp, var_dict = var_dict, Y = Y)
        
    # Will need to return both the model and the model variables for inference
    return model, var_dict

# Initialise our model, p_initial will specify any fixed values like the period P
model, var_dict = transit_model(p_initial, Y)

Now we are all set up to start performing a best-fit using PyMC.

# PyMC requires the dictionary of starting values to only include variables in the model
# So we must remove the period parameter P as we keep it fixed
p_pymc = deepcopy(p_initial)
del p_pymc["P"]

# Use PyMC's maximum posteriori optimisation function
map_estimate = pm.find_MAP(
    model = model,               # PyMC model to optimise
    include_transformed = False, # If this is true it will also output the PyMC transformed values of bounded parameters
    start = p_pymc,              # Starting point of optimisations
    maxeval = 30000,             # Maximum steps to run (normally will converge before this)
)

# Create a new dictionary of optimised values which includes our fixed parameters
p_opt = deepcopy(p_initial)
p_opt.update(map_estimate)

print("Starting log posterior value:", gp.logP(p_initial, Y))
print("New optimised log posterior value:", gp.logP(p_opt, Y))

100.00% [549/549 00:11<00:00 logp = 9,785.1, ||grad|| = 357.74]

Starting log posterior value: 9804.566510790806
New optimised log posterior value: 9826.910564388214

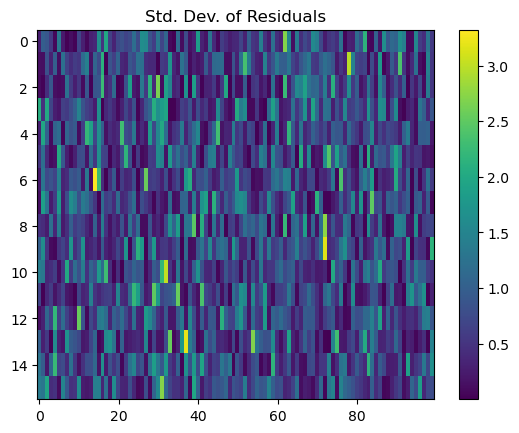
Although this probably won’t be needed for the simulated data and will likely clip no data points, luas.GP comes with a sigma_clip method which performs 2D Gaussian process regression and can clip outliers that deviate from a given significance value and replace them with the GP predictive mean at those locations (note we need to maintain a complete grid structure and cannot remove these data points).

# This function will return a JAXArray of the same shape as Y
# but with outliers replaced with interpolated values
Y_clean = gp.sigma_clip(p_opt, # Make sure to perform sigma clipping using a good fit to the data
                        Y,     # Observations JAXArray
                        5.     # Significance level in standard deviations to clip at
                       )

Number of outliers clipped =  0

For MCMC tuning with large numbers of parameters, it can be very helpful to use the Laplace approximation to select a good choice of tuning matrix or “mass matrix” for No U-Turn Sampling (NUTS). This can often return quite accurate approximations of the covariance matrix of the posterior - especially when most of the parameters are well constrained.

If outliers were clipped then optimisation may need to be ran again on the cleaned data before running this step as the Laplace approximation should be performed at the maximum of the posterior. Also note that we use the gp.laplace_approx_with_bounds method instead of gp.laplace_approx because we have bounds on some of our parameters which means PyMC will perform a transformation on these parameters we would like our Laplace approximation to take account of. See the gp.laplace_approx_with_bounds documentation for more details.

# Returns the covariance matrix returned by the Laplace approximation
# Also returns a list of parameters which is the order the array is in
# This matches the way jax.flatten_util.ravel_pytree will sort the parameter PyTree into
cov_mat, ordered_param_list = gp.laplace_approx_with_bounds(
    p_opt,               # Make sure to use best-fit values
    Y_clean,             # The observations being fit
    param_bounds,        # Specify the same bounds that will be used for the MCMC
    fixed_vars = ["P"],  # Make sure to specify fixed parameters as otherwise they are marginalised over
    return_array = True, # May optionally return a nested PyTree if set to False which can be more readable
    regularise = True,   # Often necessary to regularise values that return negative covariance
    large = False,       # Setting this to True is more memory efficient which may be needed for large data sets
)

# This function will output information on what regularisation has been performed
# And will mention if there are remaining negative values along the diagonal of the covariance matrix
# It does not however check if the covariance matrix is invertible

No regularisation needed to remove negative values along diagonal of covariance matrix.

Build our model again using the same parameters being varied and sample all parameters using NUTS. Note that PyMC has far more options for sampling here and can easily do blocked Gibbs sampling with multiple NUTS steps or you can intermix NUTS sampling with other methods such as slice sampling, etc.

PyMC appears to be unable to run JAX functions in parallel which is why cores = 1 has been set. If wanting to run in parallel then the current suggestion is to run separate programs in parallel which each runs a chain with PyMC and save each arviz inference data object separately. These can later by loaded in and combined with arviz.concat

# Initialise our PyMC model
model, var_dict = transit_model(p_opt, Y_clean)

# The NUTS step takes as input the variables created when initialising the model
# We also sort these variables in the same order our Laplace approximated covariance matrix is in
NUTS_model_vars = [var_dict[par] for par in ordered_param_list]
NUTS_step = pm.NUTS(NUTS_model_vars, scaling = cov_mat, is_cov = True, model = model)

# Begin MCMC sampling
idata = pm.sample(
    model = model,           # PyMC model to sample
    step = NUTS_step,        # Sampling steps to use (can be list for blocked Gibbs sampling)
    initvals = map_estimate, # Starting point of inference (will jitter around this location)
    draws = 1000,            # Number of samples from MCMC post warm-up
    tune = 1000,             # Number of tuning steps
    chains = 2,              # Number of chains to run
    cores = 1,               # This will probably fail if not set to 1 as I don't think PyMC can parallelise JAX functions
)

# Saves the inference object
#idata.to_json("MCMC_chains.json");

INFO:pymc:Sequential sampling (2 chains in 1 job)
INFO:pymc:NUTS: [Foot, T0, Tgrad, a, b, log_h, log_l_l, log_l_t, log_sigma, q1, q2, rho]
INFO:pymc:Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 542 seconds.

100.00% [2000/2000 04:25<00:00 Sampling chain 0, 0 divergences]

100.00% [2000/2000 04:35<00:00 Sampling chain 1, 0 divergences]

Print a summary of the samples using arviz. Important values to look at for convergence are that the effective sample size of the bulk of the distribution (ess_bulk) and the tail of the distribution (ess_tail) are at least ~500-1000 and that the Gelman-Rubin r_hat statistic is less than ~1.01 for each parameter.

az.summary(idata, round_to = 4)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
T0[0]	0.0000	0.0002	-0.0004	0.0005	0.0000	0.0000	2565.2638	1298.4558	1.0008
a[0]	8.0175	0.0465	7.9296	8.1076	0.0008	0.0006	3294.2116	1687.6763	0.9994
b[0]	0.4949	0.0082	0.4782	0.5097	0.0001	0.0001	3125.7605	1572.8233	0.9996
Foot[0]	1.0004	0.0002	1.0000	1.0008	0.0000	0.0000	1504.8016	1066.9443	0.9996
Foot[1]	1.0003	0.0002	0.9999	1.0007	0.0000	0.0000	1443.0448	1173.2878	1.0011
Foot[2]	1.0003	0.0002	0.9999	1.0008	0.0000	0.0000	1421.7851	913.5703	0.9998
Foot[3]	1.0002	0.0002	0.9998	1.0006	0.0000	0.0000	1462.9831	1235.1268	0.9997
Foot[4]	1.0002	0.0002	0.9997	1.0006	0.0000	0.0000	1440.3561	1116.3609	1.0000
Foot[5]	1.0002	0.0002	0.9997	1.0006	0.0000	0.0000	1456.9851	1302.7221	1.0003
Foot[6]	1.0002	0.0002	0.9998	1.0006	0.0000	0.0000	1418.3667	1237.7032	1.0004
Foot[7]	1.0001	0.0002	0.9997	1.0006	0.0000	0.0000	1433.9632	1319.4732	1.0003
Foot[8]	1.0001	0.0002	0.9997	1.0005	0.0000	0.0000	1510.6787	1335.3507	1.0008
Foot[9]	1.0001	0.0002	0.9997	1.0005	0.0000	0.0000	1464.7426	1423.0286	1.0012
Foot[10]	1.0001	0.0002	0.9997	1.0005	0.0000	0.0000	1494.1076	1207.3775	1.0005
Foot[11]	1.0001	0.0002	0.9996	1.0005	0.0000	0.0000	1435.9245	1280.7657	1.0028
Foot[12]	1.0000	0.0002	0.9996	1.0004	0.0000	0.0000	1584.4328	1329.4167	1.0019
Foot[13]	1.0001	0.0002	0.9997	1.0005	0.0000	0.0000	1459.9993	1074.2734	1.0009
Foot[14]	1.0000	0.0002	0.9996	1.0004	0.0000	0.0000	1592.3228	1200.9379	1.0009
Foot[15]	1.0000	0.0002	0.9996	1.0004	0.0000	0.0000	1637.1632	1249.3722	1.0013
Tgrad[0]	-0.0000	0.0001	-0.0002	0.0001	0.0000	0.0000	1452.6084	1061.3817	1.0007
Tgrad[1]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1294.1243	1107.1391	1.0010
Tgrad[2]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1316.8997	1217.2827	1.0011
Tgrad[3]	0.0001	0.0001	-0.0001	0.0002	0.0000	0.0000	1354.1070	1340.0214	0.9999
Tgrad[4]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1270.4040	1045.4393	0.9999
Tgrad[5]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1285.5170	1162.3946	0.9998
Tgrad[6]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1358.7189	1032.0615	0.9996
Tgrad[7]	-0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1322.8359	1279.2810	0.9997
Tgrad[8]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1358.3631	1077.8470	1.0002
Tgrad[9]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1343.3869	1160.0850	0.9994
Tgrad[10]	-0.0000	0.0001	-0.0002	0.0001	0.0000	0.0000	1381.5977	1106.5077	1.0003
Tgrad[11]	-0.0000	0.0001	-0.0002	0.0001	0.0000	0.0000	1335.0813	1077.1550	0.9995
Tgrad[12]	-0.0000	0.0001	-0.0002	0.0001	0.0000	0.0000	1349.1585	1033.2278	1.0013
Tgrad[13]	-0.0001	0.0001	-0.0002	0.0001	0.0000	0.0000	1408.9513	1230.3455	1.0037
Tgrad[14]	0.0000	0.0001	-0.0001	0.0002	0.0000	0.0000	1502.2927	1265.4277	1.0056
Tgrad[15]	-0.0000	0.0001	-0.0002	0.0001	0.0000	0.0000	1442.6587	1230.3455	1.0048
rho[0]	0.1023	0.0018	0.0989	0.1057	0.0000	0.0000	1568.4641	1242.9263	1.0017
rho[1]	0.1008	0.0018	0.0974	0.1041	0.0001	0.0000	1395.7583	1029.8781	1.0016
rho[2]	0.1015	0.0018	0.0984	0.1052	0.0000	0.0000	1424.4607	995.8006	1.0016
rho[3]	0.1007	0.0018	0.0974	0.1041	0.0001	0.0000	1380.7625	1107.8169	1.0017
rho[4]	0.1004	0.0018	0.0969	0.1038	0.0001	0.0000	1354.8197	1017.7590	1.0014
rho[5]	0.1003	0.0018	0.0969	0.1038	0.0000	0.0000	1406.7691	1044.1863	1.0012
rho[6]	0.1008	0.0018	0.0973	0.1039	0.0000	0.0000	1403.6424	1001.7147	1.0030
rho[7]	0.1002	0.0018	0.0969	0.1035	0.0000	0.0000	1475.2461	988.7993	1.0036
rho[8]	0.1003	0.0018	0.0968	0.1034	0.0000	0.0000	1511.0185	1006.6031	1.0019
rho[9]	0.1008	0.0018	0.0974	0.1041	0.0000	0.0000	1440.5067	954.4593	1.0008
rho[10]	0.1001	0.0018	0.0969	0.1034	0.0000	0.0000	1514.9069	1096.0763	1.0005
rho[11]	0.1001	0.0018	0.0968	0.1033	0.0000	0.0000	1512.6188	1205.4313	1.0010
rho[12]	0.0992	0.0018	0.0958	0.1024	0.0000	0.0000	1449.4061	1175.0915	1.0004
rho[13]	0.0996	0.0018	0.0962	0.1027	0.0000	0.0000	1490.5528	1159.3897	1.0007
rho[14]	0.0990	0.0018	0.0954	0.1021	0.0000	0.0000	1499.4838	1268.5811	1.0004
rho[15]	0.0988	0.0018	0.0953	0.1020	0.0000	0.0000	1443.5920	1146.4771	0.9999
q1[0]	0.6409	0.0214	0.6005	0.6811	0.0004	0.0003	2610.9253	1618.1396	1.0000
q1[1]	0.6233	0.0211	0.5844	0.6640	0.0004	0.0003	2648.4357	1211.1349	1.0024
q1[2]	0.5892	0.0213	0.5494	0.6277	0.0004	0.0003	2704.2846	1301.4949	1.0017
q1[3]	0.5786	0.0205	0.5412	0.6153	0.0004	0.0003	3296.2952	1472.6865	1.0007
q1[4]	0.5615	0.0199	0.5244	0.5981	0.0004	0.0003	2853.2840	1377.7424	1.0014
q1[5]	0.5391	0.0197	0.5014	0.5742	0.0004	0.0003	2498.1320	1283.0960	1.0025
q1[6]	0.5211	0.0188	0.4822	0.5545	0.0003	0.0002	3229.0555	1368.9970	0.9995
q1[7]	0.5073	0.0188	0.4719	0.5409	0.0003	0.0002	2935.4331	1459.0047	1.0000
q1[8]	0.4692	0.0183	0.4336	0.5017	0.0003	0.0002	3020.7971	1318.1138	1.0003
q1[9]	0.4663	0.0182	0.4326	0.4994	0.0003	0.0002	3002.9425	1340.6249	1.0027
q1[10]	0.4332	0.0167	0.4041	0.4651	0.0003	0.0002	2979.1400	1581.2821	1.0009
q1[11]	0.4305	0.0176	0.3984	0.4629	0.0003	0.0002	2956.3669	1417.2910	0.9993
q1[12]	0.4058	0.0175	0.3732	0.4376	0.0003	0.0002	2857.1311	1538.5040	1.0053
q1[13]	0.3941	0.0170	0.3626	0.4258	0.0003	0.0002	2814.9345	1218.3625	1.0006
q1[14]	0.3805	0.0164	0.3479	0.4097	0.0003	0.0002	2844.8416	1367.9174	1.0002
q1[15]	0.3627	0.0162	0.3341	0.3931	0.0003	0.0002	3473.8096	1346.5352	0.9995
q2[0]	0.4375	0.0052	0.4276	0.4470	0.0001	0.0001	2923.3256	1439.8956	1.0016
q2[1]	0.4318	0.0055	0.4208	0.4414	0.0001	0.0001	2926.7665	1290.1056	0.9998
q2[2]	0.4278	0.0056	0.4178	0.4387	0.0001	0.0001	3116.7821	1529.7387	1.0004
q2[3]	0.4210	0.0058	0.4104	0.4321	0.0001	0.0001	3186.1594	1412.4906	0.9995
q2[4]	0.4146	0.0056	0.4045	0.4251	0.0001	0.0001	3092.0721	1337.3627	0.9997
q2[5]	0.4089	0.0059	0.3978	0.4197	0.0001	0.0001	2701.5901	973.7690	1.0008
q2[6]	0.4028	0.0056	0.3910	0.4125	0.0001	0.0001	3189.9160	1274.5447	1.0006
q2[7]	0.3954	0.0057	0.3842	0.4056	0.0001	0.0001	3269.1183	1462.3821	1.0053
q2[8]	0.3904	0.0058	0.3795	0.4008	0.0001	0.0001	2666.0873	1343.8624	1.0005
q2[9]	0.3821	0.0060	0.3707	0.3930	0.0001	0.0001	3034.6970	1322.1101	1.0000
q2[10]	0.3767	0.0059	0.3660	0.3877	0.0001	0.0001	2622.2536	1353.4885	1.0044
q2[11]	0.3671	0.0057	0.3565	0.3778	0.0001	0.0001	3793.3896	1677.9424	0.9994
q2[12]	0.3596	0.0062	0.3486	0.3714	0.0001	0.0001	2510.2094	1376.9356	1.0007
q2[13]	0.3512	0.0064	0.3391	0.3627	0.0001	0.0001	3110.4488	1273.1780	1.0010
q2[14]	0.3423	0.0060	0.3305	0.3533	0.0001	0.0001	3138.9003	1373.9400	1.0034
q2[15]	0.3331	0.0062	0.3219	0.3446	0.0001	0.0001	2986.5747	1474.0797	0.9993
log_h[0]	-7.4845	0.1291	-7.7092	-7.2248	0.0038	0.0027	1218.2688	1136.4569	1.0001
log_l_l[0]	6.9402	0.1129	6.7191	7.1338	0.0028	0.0020	1598.6020	1374.9977	1.0010
log_l_t[0]	-4.4080	0.0976	-4.5789	-4.2266	0.0023	0.0016	1788.1623	1543.6887	1.0005
log_sigma[0]	-7.6806	0.0814	-7.8218	-7.5241	0.0015	0.0010	3148.6890	1501.6686	1.0022
log_sigma[1]	-7.5319	0.0704	-7.6562	-7.4032	0.0014	0.0010	2773.7669	1505.0344	1.0007
log_sigma[2]	-7.6232	0.0753	-7.7611	-7.4825	0.0014	0.0010	2876.3112	1464.1562	1.0009
log_sigma[3]	-7.6088	0.0756	-7.7415	-7.4619	0.0014	0.0010	3059.7598	1202.7219	0.9996
log_sigma[4]	-7.6388	0.0744	-7.7783	-7.5017	0.0014	0.0010	2970.3225	1592.6281	0.9995
log_sigma[5]	-7.6283	0.0760	-7.7709	-7.4836	0.0014	0.0010	2884.2464	1354.3351	1.0001
log_sigma[6]	-7.5545	0.0771	-7.6878	-7.4057	0.0014	0.0010	3064.4208	1402.6634	1.0022
log_sigma[7]	-7.6538	0.0711	-7.7915	-7.5251	0.0013	0.0009	2985.6846	1425.2549	1.0001
log_sigma[8]	-7.6453	0.0753	-7.7805	-7.5017	0.0015	0.0010	2668.6986	1669.6569	0.9999
log_sigma[9]	-7.6414	0.0755	-7.7822	-7.5068	0.0014	0.0010	2743.3340	1339.1383	1.0026
log_sigma[10]	-7.5540	0.0698	-7.6832	-7.4268	0.0012	0.0009	3195.9985	1439.1744	1.0016
log_sigma[11]	-7.5078	0.0731	-7.6331	-7.3661	0.0014	0.0010	2861.4027	1227.0987	0.9998
log_sigma[12]	-7.5894	0.0743	-7.7352	-7.4584	0.0014	0.0010	2920.9343	1386.7570	1.0000
log_sigma[13]	-7.5967	0.0751	-7.7310	-7.4518	0.0014	0.0010	2789.1062	1487.8472	1.0002
log_sigma[14]	-7.5500	0.0776	-7.6962	-7.4057	0.0015	0.0011	2676.8158	1412.8364	1.0026
log_sigma[15]	-7.7196	0.0795	-7.8641	-7.5641	0.0015	0.0011	2829.8817	1469.9315	1.0000

The arviz.plot_trace function can be very useful for visualising the marginal posterior distributions of the different parameters as well as to examine the chains and diagnose any possible convergence issues.

trace_plot = az.plot_trace(idata)
plt.tight_layout()

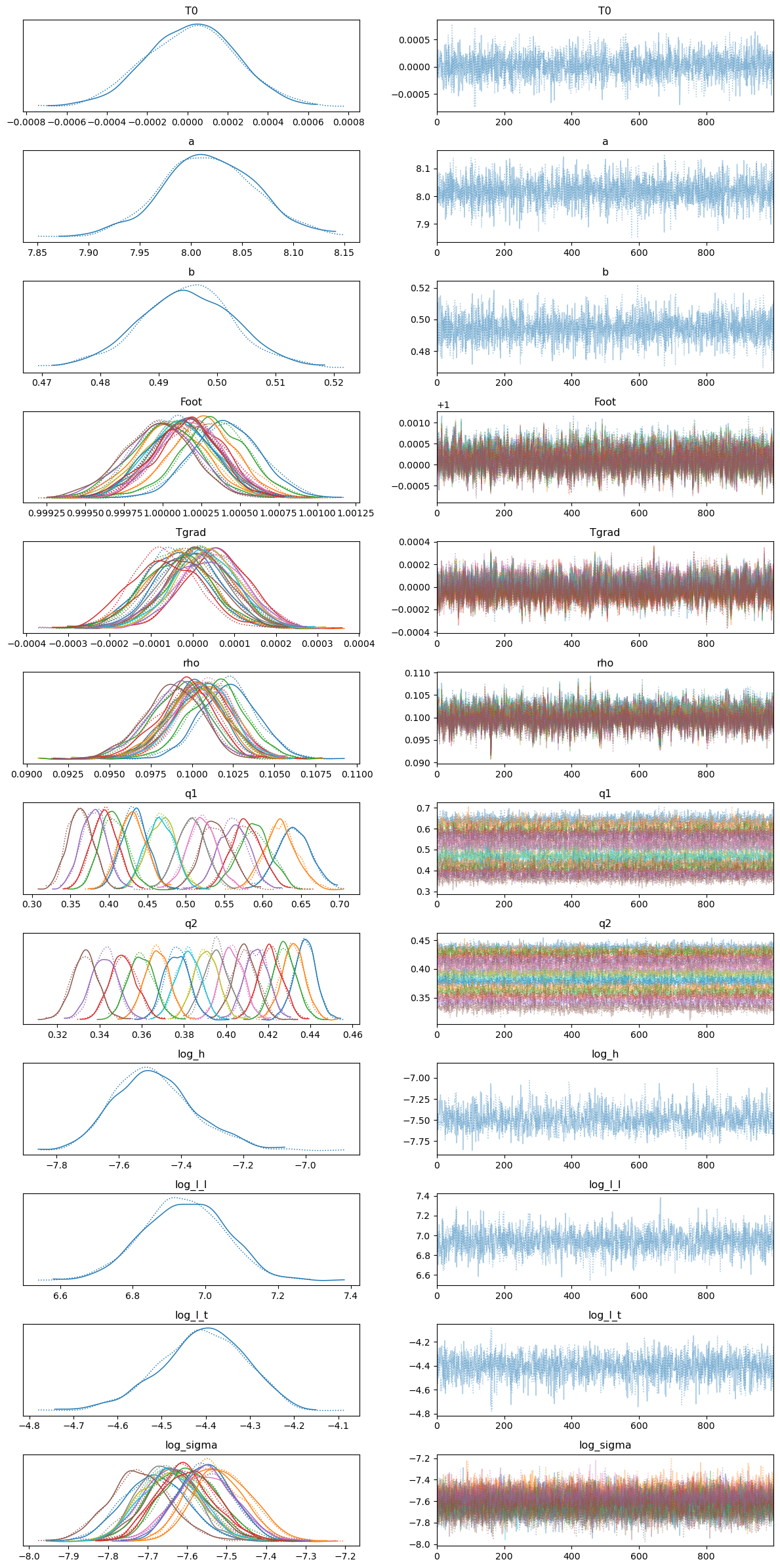
corner is great for generating nice corner plots. Unfortunately when fitting many light curves the number of parameters can make visualising the full corner plot quite unwieldly but we can always just plot subsets of parameters instead.

from corner import corner

# Select the parameters to include in the plot
params = ["T0", "a", "rho", "b", "log_h", "log_l_l", "log_l_t"]

# Plot each of the two chains separately
idata_corner1 = idata.sel(chain=[0])
idata_corner2 = idata.sel(chain=[1])

# Plot first chain
fig1 = corner(idata_corner1, smooth = 0.4, var_names = params)

# Plot second chain along with truth values
fig2 = corner(idata_corner2, quantiles=[0.16, 0.5, 0.84], title_fmt = None, title_kwargs={"fontsize": 23},
              label_kwargs={"fontsize": 23}, show_titles=True, smooth = 0.4, color = "r", fig = fig1,
              top_ticks = True, max_n_ticks = 2, labelpad = 0.16, var_names = params,
              truths = p_sim, truth_color = "k",
              )

If you want to examine the chains for any parameters you can use idata.posterior[param] to get an xarray.DataArray object and can use the to_numpy method to convert to a NumPy array. Below we retrieve the mean and covariance matrix of the radius ratio parameters and then visualise the transmission spectrum as well as the covariance matrix of the transmission spectrum.

# NumPy array of MCMC samples of shape (N_chains, N_draws, N_l)
rho_chains = idata.posterior["rho"].to_numpy()

# Get the mean radius ratio values averaged over all chains and draws
rho_mean = rho_chains.mean((0, 1))

# Calculate the covariance matrix of each chain and average together
N_chains = rho_chains.shape[0]
rho_cov = jnp.zeros((N_l, N_l))
for i in range(N_chains):
    rho_cov += jnp.cov(rho_chains[0, :, :].T)
rho_cov /= N_chains

# Standard deviation given by sqrt of diagonal of covariance matrix
rho_std_dev = jnp.sqrt(jnp.diag(rho_cov))


# We can plot our recovered spectrum against the simulated true spectrum
plt.errorbar(x_l, rho_mean, yerr = rho_std_dev, fmt = 'k.', label = "Recovered Spectrum")
plt.plot(x_l, p_sim["rho"], 'r--', label = "True Spectrum")

# Select a few samples from the MCMC to help visualise the correlation between values
rho_draws = rho_chains[0, 0:1000:100, :].T
plt.plot(x_l, rho_draws, 'k-', alpha = 0.3)
plt.xlabel("Wavelength ($\AA$)")
plt.ylabel(r"Radius Ratio $\rho$")
plt.legend()
plt.show()

plt.title("Tranmission spectrum covariance matrix")
plt.imshow(rho_cov, extent = [x_l[0], x_l[-1], x_l[-1], x_l[0]])
plt.colorbar()
plt.xlabel("Wavelength ($\AA$)")
plt.ylabel("Wavelength ($\AA$)")
plt.show()

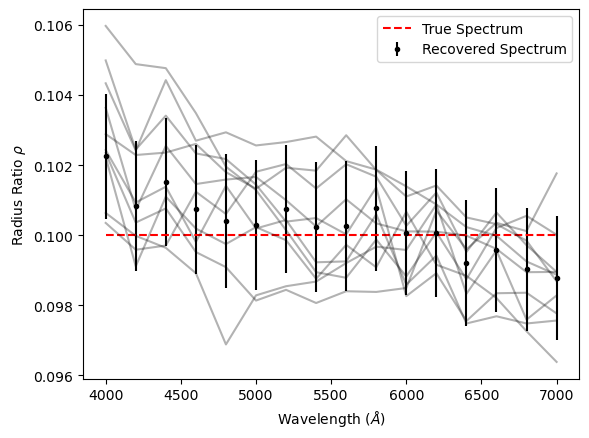
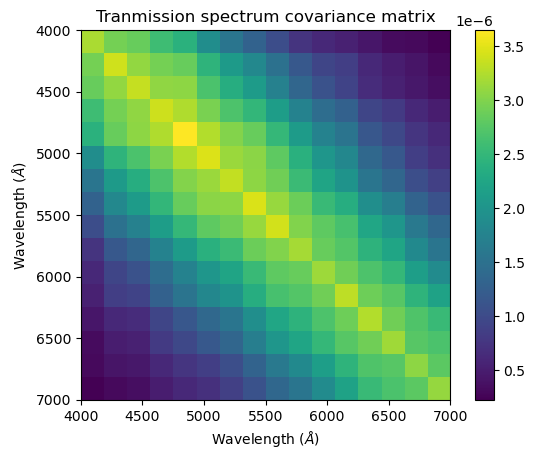
It can be hard to tell when there are significant correlations involved whether the recovered spectrum is actually consistent with the simulated spectrum. The reduced chi-squared statistic \(\chi_r^2\) is useful for determining this. It is calculated using:

\[ \begin{equation} \chi_\mathrm{r}^2 = (\bar{\vec{\rho}}_\mathrm{ret} - \vec{\rho}_\mathrm{inj})^T \mathbf{K}_\mathrm{\vec{\rho}; ret}^{-1} (\bar{\vec{\rho}}_\mathrm{ret} - \vec{\rho}_\mathrm{inj}) / N_l, \end{equation} \]

Where \(\bar{\vec{\rho}}_\mathrm{ret}\) is our retrieved mean transmission spectrum, \(\vec{\rho}_\mathrm{inj}\) is the injected transmission spectrum and \(\mathbf{K}_\mathrm{\vec{\rho}; ret}\) is our retrieved covariance matrix of the transmission spectrum.

r = rho_mean - p_sim["rho"]
chi2_r = r.T @ jnp.linalg.inv(rho_cov) @ r / N_l

print("Reduced chi-squared value:", chi2_r)

# The reduced chi-squared distribution always has mean 1 but has different standard deviations
# depending on the numbers of degrees of freedom
print("Distribution of reduced chi-squared: mean = 1, std. dev. =", jnp.sqrt(2/N_l))

Reduced chi-squared value: 0.5824927846889137
Distribution of reduced chi-squared: mean = 1, std. dev. = 0.3535533905932738